MATEMÁTICA PARA O ENEM 2

Depois de muitos pedidos, mais um material interessante para se preparar para o ENEM.

01. (UFPB ADAPTADA) A tabela a seguir apresenta a quantidade exportada de certo produto, em milhares de toneladas, no período de 2000 a 2009.

Considerando os dados apresentados na tabela, identifique as afirmativas corretas:

a) A quantidade exportada, de 2006 a 2008, foi decrescente.

b) A média da quantidade exportada, de 2003 a 2006, foi de 53 mil toneladas.

c) A moda da quantidade exportada, de 2000 a 2009, foi de 52 mil toneladas.

d) A média da quantidade exportada, de 2000 a 2004, foi menor que a média de 2005 a 2008.

e) A mediana da quantidade exportada, de 2000 a 2009, foi de 51 mil toneladas.

I. A quantidade exportada, de 2006 a 2008, foi crescente.

II. A média da quantidade exportada, de 2003 a 2006: (52 + 52 + 50 + 48)/4 = 202/4 = 50,5 milhões toneladas.

III. Entre 2000 a 2009, temos cinco vezes o número 52, logo a moda é 52.

IV. A média da quantidade exportada, de 2000 a 2004: (48 + 52 + 54 + 52 + 52)/5 = 258/5 = 51,6 milhões toneladas.

A média da quantidade exportada, de 2005 a 2008: (50 + 48 + 52 + 54 + 52)/5 = 256/5 = 51,2 milhões toneladas.

Podemos concluir que a média da quantidade exportada, de 2000 a 2004, foi maior que a média de 2005 a 2008.

V. Sabendo que a mediana é a média aritmética dos dois termos centrais e Colocando os dados em rol, temos: (48, 48, 50, 52, 52, 52, 52, 52, 54, 54).

A mediana da quantidade exportada, de 2000 a 2009 é (52 + 52)/2 = 104/2 = 52.

02. (UFPI 2003) O histograma abaixo apresenta as alturas de trinta atletas de uma equipe de futebol.

Com esses dados, podemos concluir que a média das alturas dos atletas é aproximadamente:

a) 1,58      b) 1,65      c) 1,74     d) 1,81     e) 1,92

Média = (1,55.3 + 1,6.8 + 1,75.10 + 1,85.6 + 1,95.3)/30 = 1,74.

03. (UERJ 99) Seis caixas-d’água cilíndricas iguais estão assentadas no mesmo piso plano e ligadas por registros (R) situados nas suas bases, como sugere a figura a seguir:

Após a abertura de todos os registros, as caixas ficaram com os níveis de água no mesmo plano. A altura desses níveis, em dm, equivale a:

a) 6,0       b) 6,5       c) 7,0      d) 7,5      e) 9,0

O que queremos é a média dos níveis = (8 + 3 + 5 + 10 + 9 + 7)/6 = 7 dm.

04. (ENEM 2008) No gráfico a seguir, estão especificados a produção brasileira de café, em toneladas; a área plantada, em hectares (ha), e o rendimento médio do plantio, em kg/ha, no período de 2001 a 2008.

A análise dos dados mostrados no gráfico revela que:

a) a produção em 2003 foi superior a 2.100.000 toneladas de grãos.

b) a produção brasileira foi crescente ao longo de todo o período observado.

c) a área plantada decresceu a cada ano no período de 2001 a 2008.

d) os aumentos na produção correspondem a aumentos no rendimento médio do plantio.

e) a área plantada em 2007 foi maior que a de 2001.

Perceba que, cada vez que a produção aumenta, acontece o mesmo com o rendimento médio.

05. (UNEB) O gráfico a seguir representa o resultado de uma pesquisa feita em um município, no mês de junho de 2001, a fim de analisar a redução do consumo de energia em residências, tendo em vista a meta fixada pelo governo, e com base na seguinte pergunta: “Qual a redução conseguida em relação à meta?”.

A partir dessa informação, e sabendo que o percentual para cada resposta é proporcional à área do setor que o representa, o ângulo do setor correspondente à resposta "menor" é igual a:

a) 108,3º      b) 118,8º      c) 142º      d) 151,2º      e) 160º

Total = 100 (42 + 20 + 33 + 6 = 101)

Menor ⇒ 42

I. 100 ------- 100%

   42 --------- X%

X = 4200/100 = 42%

II. 360⁰ ------ 100%

    Y ---------- 42%

Y = 15120/100 = 151,2⁰.

06. (FGV-RJ 2009) Na figura abaixo temos os gráficos das funções custo (C) e receita de vendas (R) diárias de um produto de uma empresa, em função da quantidade produzida e vendida, em número de unidades.

Podemos afirmar que:

a) o lucro será nulo somente se a quantidade produzida e vendida for 30.

b) haverá prejuízo somente quando a quantidade produzida e vendida for menor que 10.

c) o prejuízo máximo será de R$400.

d) o lucro máximo é superior a R$800.

e) haverá lucro positivo quando a quantidade produzida e vendida estiver entre 10 e 30.

I. A alternativa a é incorreta, pois o lucro é nulo também quando a quantidade produzida e vendida é 10.

II. A alternativa b é incorreta, pois há prejuízo também para quantida­des superiores a 30.

III. A alternativa c é incorreta, pois, para a quantidade 50, o prejuízo é maior que 400.

IV. A alternativa d é incorreta, pois o lucro (R – C) é inferior a 200.

V. A alternativa e é correta, pois o lucro será positivo (R – C > 0) para quantidades entre 10 e 30.

07. (UNESP 97) O gráfico mostra o resultado de uma experiência relativa à absorção de potássio pelo tecido da folha de um certo vegetal, em função do tempo e em condições diferentes de luminosidade. Nos dois casos, a função linear y = mx ajustou-se razoavelmente bem aos dados, daí a referência a m como taxa de absorção (geralmente medida em µ moles por unidade de peso por hora).

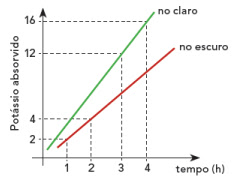
Com base no gráfico, se m₁ é a taxa de absorção no claro e m₂ a taxa de absorção no escuro, a relação entre essas duas taxas é:

a) m₁ = m₂    b) m₂ = 2m₁    c) m₁ · m₂ = 1    d) m₁ · m₂ = –1    e) m₁ = 2m₂

As retas passam na origem, pois 0 = m · 0

No claro: y = m₁x → m₁ = tg β = 12/3 = 4.

No escuro: y = m₂x → m₂ = tg α = 4/2 = 2. Daí, 2m₂= m₁.

08. (PUCCAMP-SP) A seguir vê-se parte de um gráfico que mostra o valor y a ser pago (em reais), pelo uso de um estacionamento por um período de x horas. Suponha que o padrão observado no gráfico não se altere quando x cresce.

Nessas condições, uma pessoa que estacionar o seu carro das 22 horas de certo dia até as 8 horas e 30 minutos do dia seguinte deverá pagar:

a) R$12,50     b) R$14,00     c) R$15,50    d) R$17,00    e) R$18,50

De 22h até 8h30min passaram 10h30min.

Note que o padrão é que, para cada hora, aumenta 1,5 reais. Sendo assim:

Custo de 11h = (11 – 1) · 1,5 + 2= 15 + 2 = 17 reais, passando 10h30min pagará o

mesmo.

Observação: uma formulação matemática da função seria:

ƒ(x) = (x -1).3/2 + 2, em que [x] é a parte inteira de x.

09. (UFRN) Embora o Brasil tenha uma das maiores jazidas de sal do mundo, sua produção anual em milhões de toneladas ainda é inferior à da Alemanha, da Austrália, do Canadá, da China, dos EUA, da França, da Índia e do México. O gráfico abaixo mostra a produção de sal nesses países, no ano 2000.

Considerando esses principais países produtores, a melhor aproximação do percentual de participação do Brasil na produção mundial de sal em 2000 foi de:

a) 4%    b) 5%    c) 6%    d) 11%

A produção mundial é igual a 6 + 16 + 9 + 13 + 30 + 43 + 7 + 15 + 9 = 148 milhões. Logo, a participação do Brasil é 6/148 = 0,04 ou 4%.

10. O vôlei masculino brasileiro perdeu a final olímpica em Pequim para os Estados Unidos e encerrou com medalha de prata um ciclo de glorias. Entre os jogadores que participaram dessa Olimpíada, destacam-se Andre Heller, Bruninho, Giba, André Nascimento, Serginho e Rodrigão. O gráfico seguinte apresenta a altura de cada um deles.

Determine o desvio-padrão das alturas dos seis jogadores destacados no texto.

a) 6,4       b) 7,2       c) 8,1       d) 9,0       e) 9,5

I. Média das alturas

M = (184 + 190 + 192 + 195 + 199 + 204)/6 = 1164/6 = 194 cm.

II. Variância

V = (184 – 194)² + (190 – 194)² + (192 – 194)² + (195 – 194)² + (199 – 194)² +  (204 – 194)² /6 = (100 + 16 + 4 + 1 + 25 + 100)/6 = 246/6 = 41.

III. Desvio padrão (D² = 41)

D = 6,4.

11. (UFABC 2009) O gráfico mostra a população mundial em 2000 e em 2005, e as previsões para 2015 e 2030.

Suponha que de 2030 até 2050 (quando se prevê que sete entre dez pessoas no mundo estejam vivendo nas cidades) a população mundial cresça em progressão aritmética, na qual p₁ é a população mundial prevista para 2030, p₂ a população mundial prevista para 2031, p₃ a população mundial prevista para 2032, e assim sucessivamente. Se p₂ = 8,37 bilhões de pessoas, então, em 2050, de acordo com a previsão, a população urbana, em bilhões de pessoas, será, aproximadamente, de:

a) 6,8     b) 7,7     c) 8,6     d) 9,6     e) 10,7

I. De acordo com as informações, temos:

2030 → p₁ = 8,3

2031 → p₂ = 8,37

2032 → p₃ = 8,44

2050 → p₂₁ = 8,3 + (21 – 1).0,07 = 9,7

II. A população mundial em 2050 será de 9,7 bilhões de pessoas.Logo, em 2050, a população urbana, em bilhões de pessoas, será: 7.9,7/10 = 6,79 = 6,8.

12. O curso de Turismo da "UniverCidade" realizou uma pesquisa com 1.000 turistas estrangeiros que estavam na cidade do Rio de Janeiro durante o período de Carnaval.

A partir dos dados e supondo que em cada critério da avaliação do desfile os percentuais de homens e mulheres mantenham-se os mesmos que os apresentados no gráfico de setores, pode-se afirmar que o número de mulheres que avaliaram o desfile como bom foi:

a) 400     b) 200     c) 100     d) 80      e) 40

I. Conforme o gráfico de setores, temos:

Total de turistas = 1000

40% Mulheres = 1000.40% = 400.

60% Homens = 1000.60% = 600.

II. Conforme o gráfico de barras, temos:

Mulheres que avaliaram o desfile em bom é igual a 400.20% = 80.

13. (UFSCAR 2001) Num curso de iniciação à informática, a distribuição das idades dos alunos, segundo o sexo, é dada pelo gráfico seguinte.

Com base nos dados do gráfico, pode-se afirmar que:

a) o número de meninas com, no máximo, 16 anos é maior que o número de meninos nesse mesmo intervalo de idades.

b) o número total de alunos é 19.

c) a média de idade das meninas é 15 anos.

d) o número de meninos é igual ao número de meninas.

e) o número de meninos com idade maior que 15 anos é maior que o número de meninas nesse mesmo intervalo de idade.

Conforme o gráfico, temos:

Quantidade de meninos = 2+ 1 + 4 + 2+ 1 = 10.

Quantidade de meninas = 1 + 2+ 1 + 3 + 3 = 10. (ambos apresentam a mesma quantidade de alunos por sexo)

14. Para o cálculo da inflação, utiliza-se, entre outros, o Índice Nacional de Preços ao Consumidor Amplo (IPCA), que toma como base os gastos das famílias residentes nas áreas urbanas, com rendimentos mensais compreendidos entre um e quarenta salários-mínimos. O gráfico a seguir mostra as variações do IPCA de quatro capitais brasileiras no mês de maio de 2008.

Com base no gráfico, qual item foi determinante para a inflação de maio de 2008?

a) Alimentação e bebidas.

b) Artigos de residência.

c) Habitação.

d) Vestuário.

e) Transportes.

Analisando o gráfico, verificamos que a maior variação de preços nas cidades apresentadas foi de ali­mentos e de bebidas.

15. (UFJF 2007) Um professor de Matemática elaborou, através do computador,

um histograma das notas obtidas pela turma em uma prova cujo valor era 5 pontos. Entretanto, o histograma ficou incompleto, pois esse professor esqueceu de fornecer

o número de alunos que obtiveram notas iguais a 2, 4 ou 5. Veja a ilustração a seguir.

A moda dessas notas é:

a) 1      b) 2     c) 3      d) 4     e) 5

I. Construindo a tabela

notas	Fi
0	4
1	6
2	x
3	3
4	y
5	z
Total = 40

II. Mediana = 2,5

(x₂₀ + x₂₁)/2 = 2,5; assim  x₂₀ + x₂₁ = 5,

Como a soma dos números é 5, e de acordo com a tabela, o x₂₀ = 2 e o x₂₁ = 3, portanto do elemento x₁₁ ao x₂₀ são todos iguais a 2, logo sua frequência é 10.

III. Média = 2,6

(0.4 +1.6 + 2.x + 3.3 + 4.y + 5.z)/40 = 2,6.

6 + 2x + 9 + 4y + 5z = 40.2,6

6 + 2.(10) + 9 + 4y + 5z = 104

4y + 5z = 104 – 35

4y + 5z = 69 (equação 1)

IV. Sabendo que ΣFi = 40, então temos:

4 + 6 x + 3 + y + z = 40

4 + 6 + 10 + 3 + y + z = 40

y + z = 17. (equação 2)

V. Resolvendo o sistema das equações (1) e (2):

y + z = 17 · (–4)  

4y + 5z = 69

–4y – 4z = –68  

 4y + 5z = 69

z = 1

Assim:

y + z = 17

y + 1 = 17

y = 16.

VI. Substituindo os valores de x, y e z na tabela:

notas	Fi
0	4
1	6
2	10
3	3
4	16
5	1
Total = 40

A moda é 4.

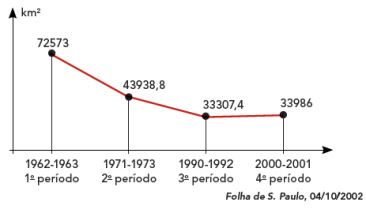
16. (FATEC 2003) No gráfico a seguir, tem-se a evolução da área da vegetação nativa

paulista, em quilômetros quadrados, nos períodos indicados.

A área, no 4o período, apresenta:

a) uma diminuição de 38.587.000m² em relação à do 1^o período.

b) uma diminuição de 39.697.000.000m² em relação à do 1^o período.

c) uma diminuição de 9.952.800m² em relação à do 2^o período.

d) um aumento de 678.600.000m² em relação à do 3^o período.

e) um aumento de 678.600m² em relação à do 3^o período.

Conforme o gráfico, no 4^o período houve um aumento de 33986 – 33307,4 = 678,6 km² = 678.600.000 m².

17. (FUVEST) Considere os seguintes dados, obtidos em 1996 pelo censo do IBGE:

i) A distribuição da população, por grupos de idade, é:

ii) As porcentagens de pessoas, maiores de 18 anos, filiadas, ou não, a sindicatos, órgãos comunitários, órgãos de classe, são:

iii) As porcentagens de pessoas, maiores de 18 anos, filiadas a sindicatos, órgãos comunitários e órgãos de classe são:

A partir dos dados anteriores, pode-se afirmar que o número de pessoas, maiores de 18 anos, filiadas a órgãos comunitários é, aproximadamente, em milhões:

a) 2     b) 6     c) 12     d) 21     e) 31

I. O número de pessoas, maiores de 18 anos, é aproximadamente 97 milhões pois totalizam 96754587 pessoas.

II. O número de pessoas, maiores de 18 anos, filiadas a órgãos comunitários é:

39% dos 31% de filiados: 39%.31% .97 = 11,7 = 12 milhões.

18. (UFMG) Fez-se uma pesquisa com um certo número de casais de uma comunidade. Esses casais foram divididos em quatro grupos, de acordo com a quantidade de filhos de cada um. Os resultados dessa pesquisa estão representados nestes gráficos:

Com base nas informações contidas nesses gráficos, é incorreto afirmar que:

a) o total de filhos dos casais do Grupo B é maior do que o total de filhos dos casais dos grupos A e C.

b) pelo menos 40% do total de filhos dos casais dos grupos A, B e C é constituído de meninos.

c) pelo menos a metade do total de filhos dos casais pesquisados é constituída de meninas.

d) mais da metade do total de filhos dos casais dos grupos A e B é constituída de meninas.

As alternativas a, b e d estão corretas. Uma sugestão para verificar isso é

considerar que foram entrevistados 100 casais, e calcular os totais indicados

nos gráficos.

No item c, a afirmação nem sempre é verdadeira, pois os casais do Grupo

D podem ter 4 ou mais filhos. Quanto mais filhos tiverem os casais desse

grupo, menor será a porcentagem de meninas em relação ao total.

19. (UFG 2008) O gráfico a seguir mostra a prevalência de obesidade da população dos EUA, na faixa etária de 20 a 74 anos, para mulheres e homens, e de 12 a 19 anos, para meninas e meninos.

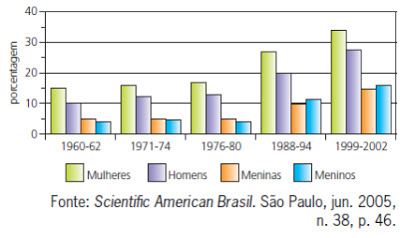
De acordo com os dados apresentados neste gráfico,

a) de 1960 a 2002, em média, 30% dos homens estavam obesos.

b) a porcentagem de meninas obesas, no período 1999-2002, era o dobro da porcentagem de meninas obesas no período 1988-1994.

c) no período 1999-2002, mais de 20% dos meninos estavam obesos.

d) no período 1999-2002, mais de 50% da população pesquisada estava obesa.

e) a porcentagem de mulheres obesas no período1988-1994 era superior à porcentagem de mulheres obesas no período 1976-1980.

Conforme o gráfico a porcentagem de mulheres obesas, no período de 1988-1994 é maior que 20% e enquanto no período 1976-1980 era menor que 20%.

20. (UFPB) Segundo dados do IBGE, as classes sociais das famílias brasileiras são estabelecidas, de acordo com a faixa de renda mensal total da família, conforme a

tabela a seguir.

Após um levantamento feito com as famílias de um município, foram obtidos os resultados expressos no gráfico a seguir.

Com base nas informações contidas no gráfico e na tabela, conclui-se que o percentual das famílias que têm renda acima de R$ 3 060,00 é de:

a) 45%      b) 60%      c) 70%     d) 85%     e) 90%

I. As famílias que têm renda acima de R$ 3 060,00 são as de classes A, B e C, conforme a tabela, que corresponde a 250 + 500 + 2250 = 3000.

II. O total de famílias: 250 + 500 + 2250 + 1500 + 500 = 5000.

III. Então temos:

5000 ----- 100%

3000 ----- x%

x = 300000/5000 = 60%.

21. (UERJ) O gráfico a seguir representa o número de pacientes atendidos mês a mês, em um ambulatório, durante o período de 6 meses de determinado ano.

O número total de pacientes atendidos durante o semestre.

a) 300    b) 320    c) 350    d) 400    e) 510

N = 60 + 40 + 60 + 40 + 20 + 80 = 300.

22. O gráfico abaixo, obtido a partir de dados do Ministério do Meio Ambiente, mostra o crescimento do número de espécies da fauna brasileira ameaçadas de extinção. Se mantida, pelos próximos anos, a tendência de crescimento mostrada no gráfico, o número de espécies ameaçadas de extinção em 2011 será igual a:

a) 465     b) 493     c) 498     d) 838     e) 899

A partir do gráfico, tendo A, B e C alinhados, temos:

(a – 461)/(2011 – 2007) = (461 – 293)/(2007 – 1983)

(a – 461)/4 = 222/24

(a – 461)/4 = 9,25

a – 461 = 4.9,25

a – 461 = 37

a = 461 + 37 = 498.

23. Assinale a alternativa que apresenta um indicador estatístico que 

pode ser obtido de uma amostra qualitativa.

a) média X    

b) mediana    

c) moda    

d) variância    

e) desvio padrão

o único que pode ser extraído de uma 

amostra qualitativa é a moda, pois se trata da qualidade 

com a maior frequência.